Запрошуємо всіх небайдужих долучитися та підтримати розвиток молодіжної культури, науки і спорту Запорізького регіону
Виклик Евкліду за межами площини: Чи можливе існування у 4-вимірному просторі?

Admin
10 Березня 2025
Розуміння неевклідової геометрії прийшло до мене не з математичних дисциплін університету, а тільки після першої самостійної поклейки шпалер).
Минулого разу ми розглянули гіпотезу Рімана, яка пов’язана з розподілом простих чисел і поведінкою дзета-функції Рімана та дізнались, що статистичні властивості нулів дзета-функції дивовижно схожі на енергетичні рівні важких атомних ядер. Тож сьогодні, продовжуючи розглядати математичні здобутки Бернхарда Рімана і його сучасників, до розгляду геометрія вищих вимірів!
На черговому занятті математичного гуртка факультету ФМКТО БДПУ учасники занурилися в захопливий світ нової нестандартної геометрії, досліджуючи питання, що виходять за межі нашого звичного тривимірного сприйняття реальності. Тема заняття «Виклик Евкліду за межами площини: Чи можливе існування у 4-вимірному просторі?» була присвячена неевклідовій геометрії та її зв’язку з багатовимірними просторами а також питанню: як змінюється паралельність, кути і відстані у просторі з іншою кривизною?
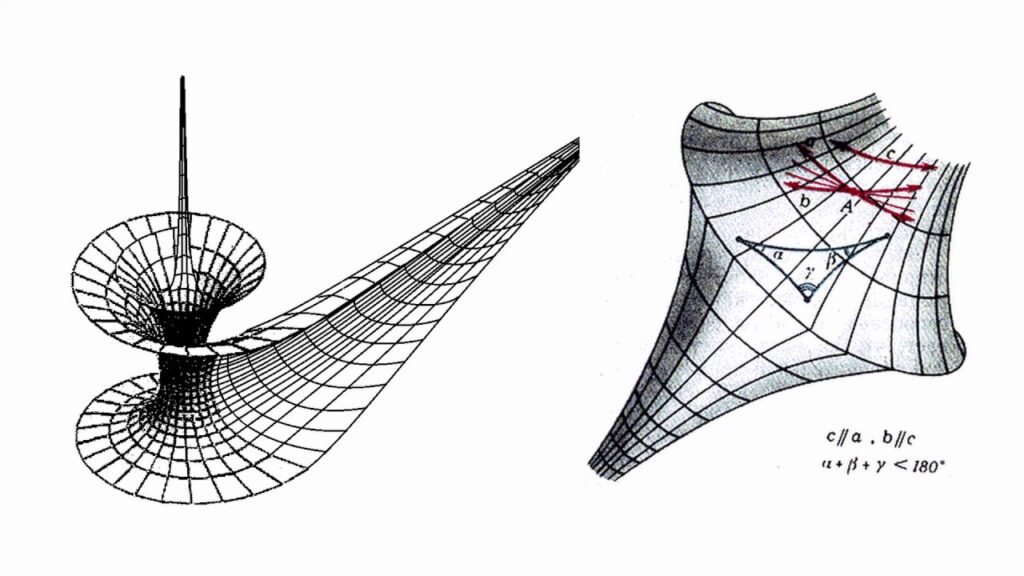
Гуртківці дізналися, що геометрія, яку ми вивчаємо в школі, базується на аксіомах Евкліда, сформульованих ще у III столітті до н.е.. Проте у XIX столітті математики Лобачевський, Бояї і Ріман зробили революційний крок, створивши геометричні системи, де паралельні прямі можуть перетинатися, а сума кутів у трикутнику не дорівнює 180 градусам. Ці теорії здавалися суто теоретичними, доки Ейнштейн не застосував їх у загальній теорії відносності, показавши, що простір навколо масивних об’єктів викривляється.
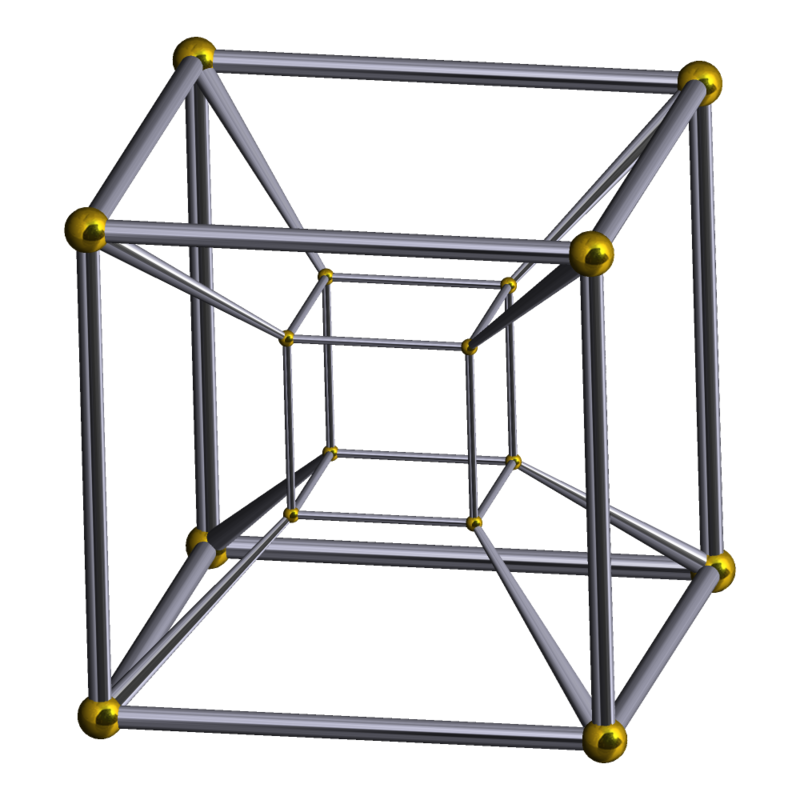
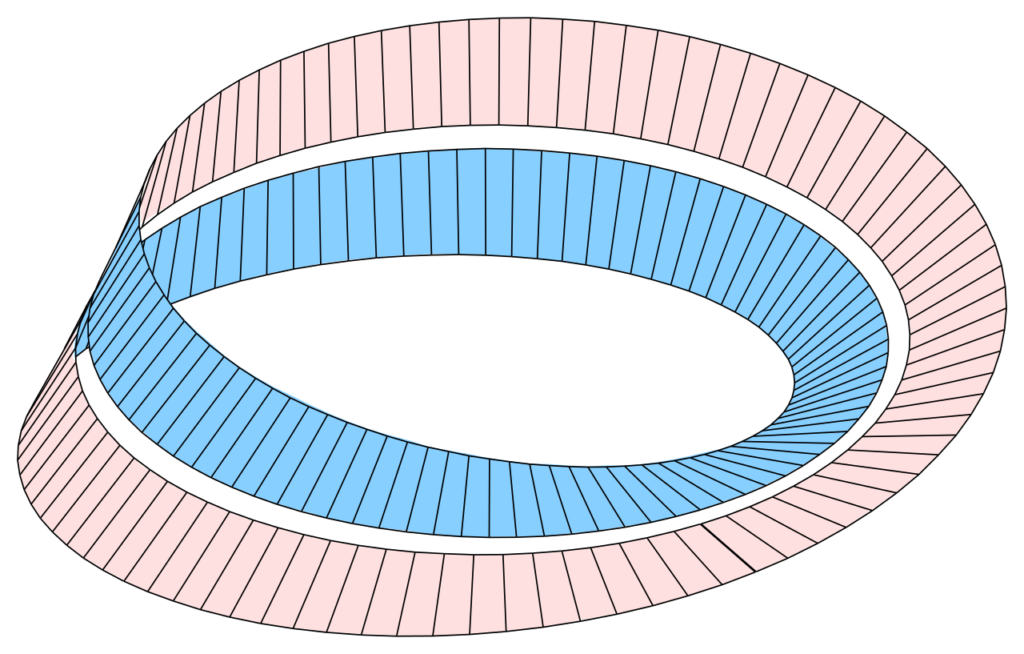
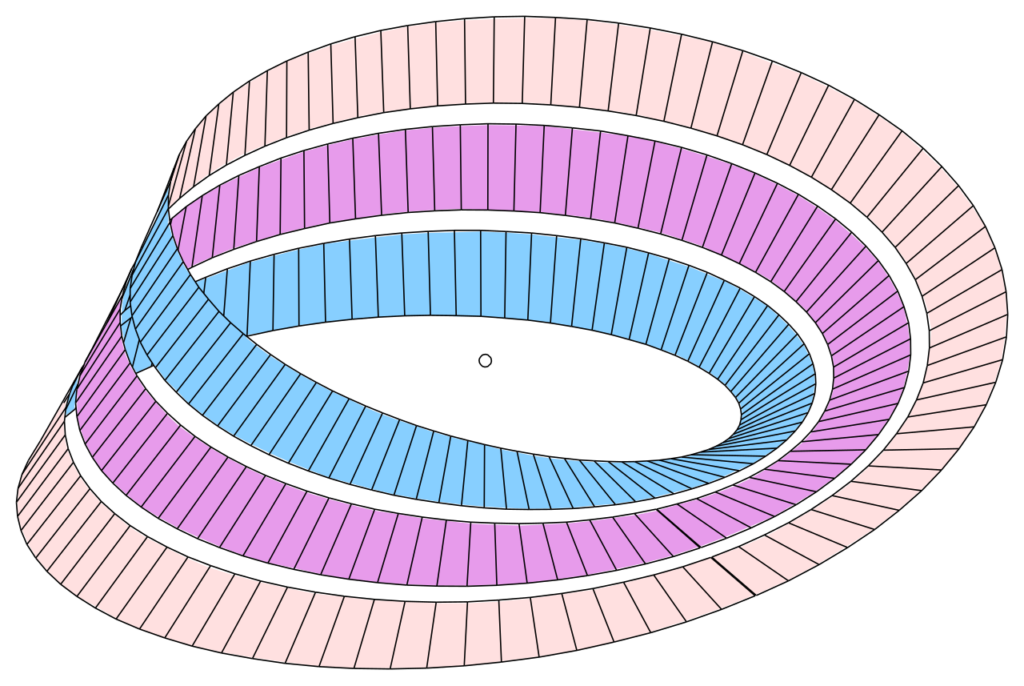
Розглянувши стрічку Мебіуса, учасники спробували уявити тесеракт або гіперкуб – чотиривимірний аналог куба, і дізналися про його проекцію у наш тривимірний світ. За допомогою моделі пляшки Клейна гуртківці розглянули властивості фігур у чотиривимірному просторі та обговорили, як би виглядало життя у такому вимірі: можливість бачити внутрішні органи без розтину, здатність виходити із замкнених кімнат без використання дверей і багато інших неймовірних можливостей.
Засідання підтвердило, що неевклідова геометрія та багатовимірні простори не лише є захопливими теоретичними концепціями, а й відіграють ключову роль у сучасній науці, відкриваючи нові перспективи для розуміння Всесвіту. Наступного разу ми продовжимо дослідження математичних світів, порушуючи не менш інтригуючі питання!



За матеріалами кафедри фізики, математики
та методики навчання

БДПУ оголошує набір на курси підвищення кваліфікації керівних та педагогічних кадрів, спеціалістів установ та закладів освіти.
Програма курсів спрямована на оновлення та поглиблення професійних знань, розвиток…
6 Січня 2026

Крок до професійної зрілості: атестація магістрантів спеціальності «Фізична культура і спорт»
У Бердянському державному педагогічному університеті відбулася атестація випускників освітньо-професійної програми…
4 Січня 2026

Психологічний клуб ФДССО - простір підтримки й відновлення
Упродовж цього півріччя діяльність Психологічного клубу здебільшого зосереджувалася на індивідуальній…
4 Січня 2026

Успішний захист кваліфікаційних робіт від штучного інтелекту до змішаного навчання в професійній освіті
Протягом грудня 2025 року проходила підсумкова атестація здобувачів ІІ (магістерського) рівня…
4 Січня 2026